google-site-verification: google44bc2b733a1a5b10.html Analisis Varians Statistika Penelitian - STATISTIKA PENDIDIKAN
» » Analisis Varians Statistika Penelitian

Analisis Varians Statistika Penelitian

Edit


ANALISIS VARIANS 


Dalam bab ini, varians akan dibahas lebih lanjut dengan terlebih dahulu melihat berbagai jenis varians kemudian menggunakannya untuk pengujian hipotesis melalui teknik analisis varians, disingkat ANAVA (ANA dari analisis dan VA dari varians).
Analisis  Variansi (ANAVA) adalah teknik analisis statistik yang dikembangkan dan diperkenalkan  pertama kali oleh Sir Ronald A. Fisher (Kennedy & Bush , 1985).
          


ANAVA dapat juga dipahami sebagai perluasan dari uji-t sehingga penggunaannya tidak terbatas kepada pengujian perbedaan dua buah rata-rata populasi, namun dapat juga untuk menguji perbedaan tiga buah rata-rata populasi atau lebih sekaligus. ANAVA adalah  tergolong analisis komparatif lebih dari dua variabel atau lebih dari dua rata-rata. Secara lebih formal, hubungan antara distribusi F dengan distribusi F dengan distribusi normal t dapat ditulis sebagai berikut :


ANAVA satu jalur (one- way ANOVA)

ANAVA satu jalur, disebut demikian karena analisis tersebut melibatkan hanya satu peubah bebas. Secara rinci, ANAVA satu jalur digunakan dalam suatu penelitian yang memiliki ciri-ciri berikut :
1. Melibatkan hanya satu peubah bebas dengan dua kategori (tingkatan) atau lebih yang dipilih dan ditentukan oleh peneliti secara tidak acak. Kategori yang dipilih disebut tidak acak karena peneliti tidak bermaksud menggenarilisasikan hasilnya ke kategori (tingkatan) lain diluar yang diteliti pada peubah itu. Sebagai contoh, peubah jenis kelamin terdiri hanya atas dua kategori (pria, wanita) atau peneliti hendak membandingkan keberhasilan antara metode A, B, dan C dalam meningkatkan kesadaran hukum masyarakat desa tanpa bermaksud menggenarilisasikannya ke metode lain di luar ketiga metode tersebut


2. Perbedaan antara kategori atau tingkatan pada peubah bebas dapat bersifat kualitatif atau kuantitatif. Pria dan wanita merupakan contoh peubah yang berbeda secara kualitatif, sedangkan kategori pada peubah jumlah tugas terstruktur perminggu (misalnya, 1 kali, 2 kali, dan 3 kali) berbeda secara kuantitatif

3. Setiap objek merupakan anggota dari hanya satu kelompok (kategori) pada peubah bebas, dan dipilih secara acak dari populasi tertentu

1.       JENIS VARIANS

Secara umum varians dapat digolongkan kedalam varians sistematik dan varians galat. Varians sistimatik adalah variasi pengukuran karena adanya pengaruh yang menyebabkan skor atau nilai data lebih condong ke satu arah tertentu dibandingkan kea rah lain. Setiap pengaruh alami atau buatan manusia yang menyebabkan terjadinya peristiwa dapat diduga atau diramalkan dalam arah tertentu, merupakan pengaruh sistematik sehingga menyebabkan terjadinya varians sistematik. Cara mengajar yang dilakukan seorang ahli secara sistematik mempengaruhi kemajuan anak didik lebih baik bila dibandingkan dengan kemajuan anak yang diajar sembarangan, hasil skor ujiannya menggambarkan adanya varians sistematik.


Salah satu jenis varians sistematik dalam kumpulan data hasil penelitian adalah varians antar kelompok atau kadang-kadang disebut pula varians eksperimental. Varians ini menggambarkan adanya perbedaan atau variasi sistematik antara kelompok-kelompok hasil pengukuran. Dengan demikian varians ini terjadi karena adanya perbedaan antara kelompok-kelompok individu.


 Contoh :  

Misalkan ada empat kelas siswa, tiap kelas banyak muridnya sama, sedang belajar Inggris, masing-masing kelas diajar oleh seorang guru dan tiap guru menggunakan metoda mengajar yang berbeda, sebut A, B, C dan D. Nilai hasil ujian akhir proses belajar untuk tiap metoda, rata-rata seperti berikut :


Metoda
A
B
C
D
Rata-rata
67,3
76,5
56,9
63,7



Aggap rata-rata ini sebagai data biasa lalu hitung variansnya; diperoleh varians antar kelompok A, B, C, dan D. Besarnya dihitung sebagai berikut. Karena tiap kelas banyak muridnya sama, maka :

Rata –rata untuk keempat rata-rata itu :



Jumlah kuadrat-kuadrat (JK) dikoreksi, yaitu setiap data dikurangi rata-ratanya lalu dikuadratkan, dan kemudian dijumlahkan, adalah :




Bagi oleh derajat kebebasannya, ialah banyak kelompok dikurangi satu, jadi 4 – 1 = 3, diperoleh varians antar kelompok A, B, dan D sebesar 66,67.



Contoh :

Misalkan dua jenis makanan ayam, (sebut A dan B) dicobakan ; A terhadap 5 ekor ayam dan B terhadap 4 ekor ayam. Segala karakteristik ke-9 ekor ayam itu (misalnya besarnya, jenisnya, umurnya dan lain-lain) sama. Setelah 20 hari percobaan pertambahan berat dagingnya (dalam ons) ditimbang dan dicatat. Hasilnya seperti berikut :


Makanan A
3,2
3,7
3,9
3,6
3,5
Makanan B
2,2
2,9
2,5
2,4
-


Pertambahan berat daging karena kedua jenis makanan itu, rata-ratanya masing-masing  dan .Rat-rata ini berbeda, bervariasi sehingga kita katakan ada varians antar kelompok.


Kita hitung dulu varians ini sebagai berikut.
Karena ukuran sample berbeda, maka rata-rata untuk kedua rata-rata di atas adalah :


Jumlah kuadrat (JK) dikoreksi untuk makanan A adalah  dan JK dikoreksi untuk makanan B adalah  .JK dikoreksi untuk kedua rata-rata antar kelompok ini adalah 1,152 + 1,44 = 2,592. Jika JK dikoreksi ini dibagi oleh derajat kebebasan kedua rata-rata, ialah (2 - 1) = 1, diperoleh varians antar kelompok 2,592.

Sekarang gabungkan ke-9 buah data itu lalu hitung variansnya. Dengan jalan ini kita peroleh varians lain yang dinamakan varians total. Untuk menghitung varians total, seperti biasa digunakan rumus yang untuk itu diperlukan rata-rata ke-9 data, setelah dihitung besarnya 3,1.

JK koreksi total untuk ke-9 data itu adalah


Setelah dibagi oleh derajat kebebasannya, ialah (9 – 1) = 8 diperoleh varians total sebesar 0,39. Varians total ini berisikan semua sumber variasi dalam skor yang sudah diketahui satu diantaranya adalah varians antar kelompok.
Mari kita cari jenis varians lainnya.


Untuk ini kita hitung varians makanan A dan varians makanan B lalu dicari rata-ratanya. Yang diperoleh adalah varians lain yang dinamakan varians dalam kelompok atau kadang-kadang disebut juga varians galat. Perhitungannya adalah sebagai berikut :



JK dikoreksi untuk data makanan A adalah :

(3,2 – 3,58)2 + . . . + (3,5 – 3,58)2 = 0,268

sedangkan
JK dikoreksi untuk data makanan B adalah :

(2,2 – 2,50)2 + . . . + (2,4 – 2,50)2 = 0,26

Kedua JK ini jumlahnya  = 0,528.
Bagi oleh derajat kebebasannya, ialah
 7 (=9 – 2) menghasilkan varians dalam kelompok 0,0754.


Dari contoh di atas diperoleh kenyataan berikut :
JK koreksi antar kelompok = 2,592 dan
JK koreksi dalam kelompok = 0,528 yang jika dijumlahkan menghasilkan 3,12. Jumlah ini sama dengan JK koreksi total. Memang demikian bahwa untuk jumlah koreksi ini berlaku aturan :
JK total = JK antar kelompok + JK dalam kelompok.........................XIV(1)


ANALISIS VARIANS SATU ARAH


Dalam bagian ini akan dibahas perluasan, yaitu menguji kesamaan k, (k > 2), buah rata-rata populasi. Tepatnya, misalkan kita mempunyai k, (k > 2), buah populasi yang masing-masing berdistribusi independent dan normal dengan rata-rata µ1, µ2, µ3,..., µk   dan  simpangan  baku berturut-turut  Akan diuji hipotesis nol Ho dengan tandingan H1


Selain daripada asumsi kenormalan tentang populasi, untuk pengujian ini juga akan dimisalkan bahwa populasi bersifat homogen ialah bahwa 


 Dari tiap populasi secara independent kita ambil sebuah sampel acak, berukuran  dari populasi kesatu,  dari populasi kedua dan seterusnya berukuran  dari populasi ke k
Data sampel akan dinyatakan dengan  yang berarti data ke-j dalam sampel yang diambil dari populasi ke-i. Untuk memudahkan, sebaiknya data sampel disusun seperti dalam daftar XIV (1).


Daftar XIV(1)

Data Sampel Dari k Buah Populasi Berdistribusi Normal



Untuk  menguji Ho melawan H1 yang kita bicarakan, varians-varians inilah yang akan digunakan, tepatnya varians antar kelompok dan varians dalam kelompok.  Dengan persyaratan tentang populasi seperti tersebut di atas, ternyata bahwa rasio varians antar kelompok terhadap varians dalam kelompok membentuk  statistic F, tepatnya 




Statistik inilah yang digunakan untuk menguji Ho.

Jika kedua varians dalam statistic F di atas dituliskan menggunakan jumlah kuadrat, maka rumus XIV(2) untuk menguji Ho berubah menjadi

Ternyata bahwa statistik di atas berdistribusi F dengan dk pembilang  dan dk penyebut  .Kriteria pengujian adalah: tolak  jika  dimana  dapat dilihat dari daftar distribusi F dengan peluang  dan dk = . disini  taraf nyata untuk pengujian.

Untuk memudahkan perhitungan, rumus XIV(3) diubah seperlunya dan akan digunakan simbul-simbul berikut :


R.,A.,D.,dan  merupakan jumlah kuadrat-kuadrat (JK) yang berturut-turut berdasarkan sumber-sumber variasi rata-rata, antar kelompok, dalam kelompok, dan total. Setiap JK sumber variasi didampingi oleh derajat kebebasan (dk). Untuk rata-rata dk=1, untuk antar kelompok dk=(k - 1), untuk dalam kelompok  dan untuk total .


Jika tiap JK dibagi derajat kebebasannya masing-masing, diperoleh varians untuk masing-masing sumber variasi yang disini akan disebut kuadrat tengah (KT). Dengan jalan membagi KT antar kelompok oleh KT dalam kelompok, maka diperoleh harga:


Yang dapat digunakan untuk menguji hipotesis kesamaan beberapa rata-rata populasi. Jika harga F ini lebih besar dari F daftar dengan dk pembilang (k - 1) dan dk penyebut  untuk   yang dipilih, maka hipotesis nol  kita tolak. 

Analisis untuk menguji kesamaan k buah rata-rata populasi yang dibicarakan di sini dikenal dengan analisis varians satu arah. Dinamakan demikian karena analisisnya menggunakan varians dan data hasil pengamatan merupakan pengaruh satu factor.



Contoh :

Empat macam campuran makanan diberikan kepada kambing dalam rangka percobaan untuk meningkatkan pertambahan berat dagingnya. Setelah percobaan selesai, pertambahan berat dagingnya dicatat dan hasilnya sebagai berikut.


DAFTAR XIV(3)
PERTAMBAHAN BERAT DAGING KAMBING (DALAM KG)
SETELAH PERCOBAAN SELESAI




Kita misalkan , bahwa pertambahan berat berdistribusi normal dan dalam bagian Bagian 16,  Bab XII, dalam contoh untuk data yang sama tidak diuji bahwa populasinya mempunyai varians yang homogen.




DAFTAR XIV(4)
DAFTAR ANALISIS VARIANS PERTAMBAHAN BERAT DAGING KAMBING KARENA 4 MACAM MAKANAN

Sumber Variasi
dk
JK
KT
F

Rata-rata

Antar Kelompok

Dalam Kelompok

1

3

14

4355,56

10,24

372,20

4355,56

3,41

26,59

0,128
Total
18
4738
-
-


Dengan Rumus XIV(4) didapat harga F = 0,128.

 Dari daftar distribusi F dengan dk pembilang 3 dan dk penyebut 14 dan peluang 0,96 (jadi  0,05) didapat F=3,34. Ternyata bahwa F=0,128 lebih kecil dari 3,34; jadi hipotesis  diterima dalam taraf nyata 0,05. Keempat macam campuran makanan itu menyebabkan pertambahan berat badan kambing yang tidak berbeda secara nyata. Dengan kata lain, keempat macam makanan itu sama efektifnya sehingga campuran mana saja yang digunakan akan memberikan hasil yang secara nyata tidak berbeda.


Anava Satu Jalur 


ANOVA

Analisis  Variansi (ANAVA) adalah teknik analisis statistik yang dikembangkan dan diperkenalkan  pertama kali oleh Sir Ronald A. Fisher (Kennedy & Bush , 1985).


ANAVA dapat juga dipahami sebagai perluasan dari uji-t sehingga penggunaannya tidak terbatas kepada pengujian perbedaan dua buah rata-rata populasi, namun dapat juga untuk menguji perbedaan tiga buah rata-rata populasi atau lebih sekaligus. ANAVA adalah  tergolong analisis komparatif lebih dari dua variabel atau lebih dari dua rata-rata. Secara lebih formal, hubungan antara distribusi F dengan distribusi F dengan distribusi normal t dapat ditulis sebagai berikut: 


ANAVA satu jalur (one- way ANOVA)

ANAVA satu jalur, disebut demikian karena analisis tersebut melibatkan hanya satu peubah bebas. Secara rinci, ANAVA satu jalur digunakan dalam suatu penelitian yang memiliki ciri-ciri berikut:


1. Melibatkan hanya satu peubah bebas dengan dua kategori (tingkatan) atau lebih yang dipilih dan ditentukan oleh peneliti secara tidak acak. Kategori yang dipilih disebut tidak acak karena peneliti tidak bermaksud menggenarilisasikan hasilnya ke kategori (tingkatan) lain diluar yang diteliti pada peubah itu. Sebagai contoh, peubah jenis kelamin terdiri hanya atas dua kategori (pria, wanita) atau peneliti hendak membandingkan keberhasilan antara metode A, B, dan C dalam meningkatkan kesadaran hukum masyarakat desa tanpa bermaksud menggenarilisasikannya ke metode lain di luar ketiga metode tersebut.

2. Perbedaan antara kategori atau tingkatan pada peubah bebas dapat bersifat kualitatif atau kuantitatif. Pria dan wanita merupakan contoh peubah yang berbeda secara kualitatif, sedangkan kategori pada peubah jumlah tugas terstruktur perminggu (misalnya, 1 kali, 2 kali, dan 3 kali) berbeda secara kuantitatif.

3. Setiap objek merupakan anggota dari hanya satu kelompok (kategori) pada peubah bebas, dan dipilih secara acak dari populasi tertentu. 


LANGKAH-LANGKAH MENJAWAB :

1. Diasumsikan bahwa data dipilih secara random, berdistribusi normal, dan variannya homogen.

 2. Hipotesis  dalam bentuk kalimat.
 = Terdapat perbedaan yang signifikan antara kelompok A, kelompok B, dan kelompok C.
  = Tidak ada perbedaan yang signifikan antara kelompok A, kelompok B, dan kelompok C

 3. Hipotesis  dalam bentuk statistik
  ; 

4. Daftar statistik induk

No
Kelompok A
Kelompok B
Kelompok C
1
63
53
31
2
77
60
84
3
63
57
56
4
47
40
84
5
70
40
54
6
57
50
76
7
60
80
88
8
77
57
84
9
60
75
54
10
80
60
70
11
67
80
64
12
73
63
75
13
73
50
60
14
67
80
50
15
93
70
84
16
83
50
68
17
80
67
67
18
57
76
54
19
57
70
60
20
73
67
62
21
47
53
60
22
50
60
55
23
50
77
86
24
70
43
88
25
60
63
53
26
83
87
60
27
53
63
61
28
90
83
72
29
60
50
68
30
73
83
88
31
80
53
76
32
70
67
60
33
53
53
72
34
50
66
82
35
70
73
73
36
60
70
64
37
93
77
70
38
77
53
72
39
72
50
40
70




 1. Menghitung jumlah kuadrat antar group  dengan rumus:








2. Hitunglah derajat bebas antar group dengan rumus:
 jumlah group A

 3. Hitunglah kuadrat rerata antar group  dengan rumus:

4. Hitunglah jumlah kuadrat dalam antar group  dengan rumus:






5. Hitunglah derajat bebas dalam group dengan rumus:
 = N - A = 117 - 3 = 114

 6. Hitunglah kuadrat rarata dalam antar group  dengan rumus:

7. Carilah  dengan rumus:

8. Tentukan taraf signifikansinya, misalnya  = 0,05

 9. Cari  dengan rumus:





10. Tentukan kriteria pengujian: jika  maka terima 

Kesimpulan

Maka terima H0, artinya dapat disimpulkan bahwa tidak terdapat perbedaan rata-rata hasil belajar antara kelompok A, kelompok B, dan kelompok C
Daftar Pustaka
Sudjana.2002.Metoda Statistika.Tarsito : Bandung.

Subscribe to receive free email updates:

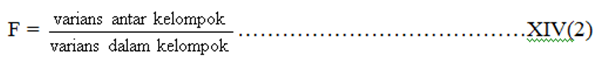
0 Response to "Analisis Varians Statistika Penelitian"

Post a Comment

Subscribe to: Post Comments (Atom)